Φ
'Il rapporto Aureo
è una dimostrazione meravigliosa del fatto che
l’uomo creatore e la natura
si servono degli stessi strumenti
nel creare le forme per arrivare alla bellezza'
Cos'è la sezone aurea?
—La sezione aurea è la parte di segmento media porporzionale tra la lunghezza totale del segmento e la parte restante.
(a+b) : a = a : b
Il rapporto aureo indica il rapporto fra due lunghezze disuguali, delle quali la maggiore è medio proporzionale tra la minore e la somma delle due. Lo stesso rapporto esiste anche tra la lunghezza minore e la loro differenza.
Risolviamo algebricamente
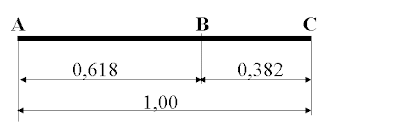
AC
= 1 AB
= x BC
= (1– x)
quindi:
1 :
x = x
: (1 – x)
per la proprietà fondamentale delle proporzioni
x2 = (1 –
x)
x2
+ x – 1 = 0
da cui si ricava:
scartando la soluzione negativa
in quanto siamo di fronte a segmenti
Il rapporto di SEZIONE AUREA ed è
un numero irrazionale corrispondente a 0,618………
con infinite cifre dopo la virgola
Il reciproco di 1/x=1+x viene indicato con e vale circa 1,618…. indicato come RAPPORTO AUREO
IL RETTANGOLO AUREO
Le sue proporzioni sono basate sul RAPPORTO AUREO
a : b= b: (a-b)
E' una particolare figura in cui il lato maggiore e il minore stanno tra loro in un rapporto pari a Φ.
Costruzione dei rettangolo aureo
- Si trova poi il punto medio di un lato e si punta su di esso un compasso con apertura sino a un vertice non adiacente del quadrato.
- Il punto nel quale la circonferenza così determinata interseca il prolungamento del lato determina il secondo estremo del lato maggiore del rettangolo
al contrario da un rerttangolo aureo se si prova a sottrarre un'area pari al quadrato generato dal lato minore, si otterrà un nuovo rettangolo ancora una volta in proporzione aurea.
Togliendo ancora un quadrato dal rettangolo «figlio» con lo stesso procedimento, si otterrà nuovamente un rettangolo rimpicciolito del fattore Φ.
Proseguendo, si otterranno dunque una serie di rettangoli sempre più piccoli, ma tutti simili.
Un modo per costruire questo tipo di rettangolo è quello di accostare in successione di quadrati che abbiamo per lati i valori della successione di Fibonacci.
In questo modo si creerà una successione di rettangoli aurei.
La spirale logaritmica è caratterizzata dal fatto che le distanze fra i bracci della spirale aumentano secondo una progressione geometrica; utilizzando i numeri di Fibonacci, si può ottenere dunque un particolare tipo di spirale logaritmica.
Riconsiderando il rettangolo aureo e la sua suddivisione in figure minori e simili, è possibile ottenere la creazione di questa spirale: essa è generata da archi di circonferenza che hanno come raggi i lati dei quadrati costruiti sui lati minori. La spirale si sviluppa intorno a un punto detto «occhio di Dio», ossia il punto d’incontro tra le due diagonali che si intersecano in ciascuna coppia di rettangoli.
Un numero irrazionale particolare
nSimbolo della scuola pitagorica
è la stella a 5 punte formata dalle diagonali di un pentagono regolare
Le diagonali si intersecano formando un nuovo pentagono regolare dentro cui si forma una nuova stella a 5 punte ……………
e questo può continuare all’INFINITO
nQuindi si possono costruire infinite figure regolari dentro la figura regolare di partenza
Ma osserviamo da vicino:
e....
Il Lato è la SEZIONE AUREA della Diagonale
quindi nel PENTAGONO
simbolo della scuola pitagorica
troviamo
nInfinite sezione auree tra lato e diagonale della figura
nInfinite sezioni auree tra lati dei nuovi pentagoni e il lato del pentagono di partenza
L'infinito presente nella figura geometrica finita è un numero irrazionale che si ripete armonicamente e indefinitamente
